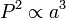soal latihan mid test

soal latihan mid semester dapat dikerjakan disini

sudut rotasi bumi

sudut rotasi

sudut rotasi bumi 23 derajat disebabkan oleh tabrakan bumi dengan asteroid

menyingkap alam semesta

silakan baca disini 
menyingkap alam semesta

blackhole and white hole

animasinya klik disini

hubungan hukum kepler dengan hukum newton

Hukum Pertama

Figure 2: Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips.

"Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya."

Pada zaman Kepler, klaim di atas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.
Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproksimasi lingkaran. Jadi, kalau ditilik dari pengamatan jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit-orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari Matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh, Pluto, yang diamati pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elips dan kecil ukurannya.

Hukum Kedua

Figure 3: Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat di dekat Matahari dan lambat di jarak yang jauh. Sehingga, jumlah area adalah sama pada jangka waktu tertentu.

"Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."

Secara matematis:

dimana adalah "areal velocity".

Hukum Ketiga

Planet yang terletak jauh dari Matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepler ketiga menjabarkan hal tersebut secara kuantitatif.

"Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari Matahari."

Secara matematis:

dengan adalah perioda orbit planet dan adalah sumbu semimajor orbitnya.
Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar Matahari.

Eyang Newton juga menunjukkan bahwa Hukum III Kepler juga bisa diturunkan secara matematis dari Hukum Gravitasi Universal dan Hukum Newton tentang gerak dan gerak melingkar. Sekarang mari kita tinjau Hukum III Kepler menggunakan pendekatan eyang Newton.
Terlebih dahulu kita tinjau kasus khusus orbit lingkaran, yang merupakan kasus khusus dari orbit elips. Semoga dirimu belum melupakan Hukum Newton dan pelajaran Gerak Melingkar…
Kita tulis kembali persamaan Hukum II Newton :


Pada kasus gerak melingkar beraturan, hanya terdapat percepatan sentripetal, yang besarnya adalah :


Kita tulis kembali persamaan Hukum Gravitasi Newton :


Sekarang kita masukan persamaan Hukum Gravitasi Newton dan percepatan sentripetal ke dalam persamaan Hukum II Newton :


m₁ adalah massa planet, m_M adalah massa matahari, r₁ adalah jarak rata-rata planet dari matahari, v₁ merupakan laju rata-rata planet pada orbitnya.
Waktu yang diperlukan sebuah planet untuk menyelesaikan satu orbit adalah T₁, di mana jarak tempuhnya sama dengan keliling lingkaran,2phir₁. Dengan demikian, besar v₁ adalah :


Kita masukan persamaan v₁ ke dalam persamaan di atas :


Misalnya persamaan 1 kita turunkan untuk planet venus (planet 1). Penurunan persamaan yang sama dapar digunakan untuk planet bumi (planet kedua).


T₂ dan r₂ adalah periode dan jari-jari orbit planet kedua. Sekarang coba anda perhatikan persamaan 1 dan persamaan 2. Perhatikan bahwa ruas kanan kedua persamaan memiliki nilai yang sama. Dengan demikian, jika kedua persamaan ini digabungkan, akan kita peroleh :




Kita juga bisa menurunkan persamaaan untuk menghitung besarnya periode gerak planet (T) dengan cara lain. Pertama terlebih dahulu kita turunkan untuk kasus gerak melingkar.
Sebelumnya kita telah mensubtitusikan persamaan Hukum Gravitasi Newton dan percepatan sentripetal ke dalam persamaan Hukum II Newton :


Pada pembahasan mengenai gerak melingkar beraturan, kita mempelajari bahwa laju v adalah perbandingan jarak tempuh dalam satu kali putaran dengan periode (waktu yang dibutuhkan untuk melakukan satu kali putaran), yang secara matematis dirumuskan sebagai berikut :


Kita subtitusikan nilai v pada persamaan laju untuk orbit lingkaran, ke dalam persamaan T :


Pada persamaan ini tampak bahwa periode dalam orbit lingkaran sebanding dengan pangkat 3/2 dari jari-jari orbit. Eyang Newton menunjukkan bahwa hubungan ini juga berlaku untuk orbit elips, di mana jari-jari orbit lingkaran (r) diganti dengan setengah sumbu utama a




DATA ASTRONOMI

Sumber Artikel : http://www.gurumuda.com

blck hole menurut Al Qur'an

silakan klik dibawah ini tentang black hole menurut Al Qur an :

black hole menurut Al Qur'an

hubungan black hole dan quantum

black hole quantum

black hole

 Lubang hitam (black hole ) adalah sebuah pemusatan massa yang cukup besar sehingga menghasilkan gaya gravitasi yang sangat besar. Gaya gravitasi yang sangat besar ini mencegah apa pun lolos darinya kecuali melalui perilaku terowongan kuantum. Medan gravitasi begitu kuat sehingga kecepatan lepas di dekatnya mendekati kecepatan cahaya. Tak ada sesuatu, termasuk radiasi elektromagnetik yang dapat lolos dari gravitasinya, bahkan cahaya hanya dapat masuk tetapi tidak dapat keluar atau melewatinya, dari sini diperoleh kata "hitam". Istilah "lubang hitam" telah tersebar luas, meskipun ia tidak menunjuk ke sebuah lubang dalam arti biasa, tetapi merupakan sebuah wilayah di angkasa di mana semua tidak dapat kembali. Secara teoritis, lubang hitam dapat memliki ukuran apa pun, dari mikroskopik sampai ke ukuran alam raya yang dapat diamati.

Asal-mula lubang hitam

Lubang Hitam tercipta ketika suatu obyek tidak dapat bertahan dari kekuatan tekanan gaya gravitasinya sendiri. Banyak obyek (termasuk matahari dan bumi) tidak akan pernah menjadi lubang hitam. Tekanan gravitasi pada matahari dan bumi tidak mencukupi untuk melampaui kekuatan atom dan nuklir dalam dirinya yang sifatnya melawan tekanan gravitasi. Tetapi sebaliknya untuk obyek yang bermassa sangat besar, tekanan gravitasi-lah yang menang.

Massa dari lubang hitam terus bertambah dengan cara menangkap semua materi didekatnya. Semua materi tidak bisa lari dari jeratan lubang hitam jika melintas terlalu dekat. Jadi obyek yang tidak bisa menjaga jarak yang aman dari lubang hitam akan terhisap. maybe one day, the thing will haappen with sun, moonth, and our world be able to be dark Berlainan dengan reputasi yang disandangnya saat ini yang menyatakan bahwa lubang hitam dapat menghisap apa saja disekitarnya, lubang hitam tidak dapat menghisap material yang jaraknya sangat jauh dari dirinya. dia hanya bisa menarik materi yang lewat sangat dekat dengannya. Contoh : bayangkan matahari kita menjadi lubang hitam dengan massa yang sama. Kegelapan akan menyelimuti bumi dikarenakan tidak ada pancaran cahaya dari lubang hitam, tetapi bumi akan tetap mengelilingi lubang hitam itu dengan jarak dan kecepatan yang sama dengan saat ini dan tidak terhisap masuk kedalamnya. Bahaya akan mengancam hanya jika bumi kita berjarak 10 mil dari lubang hitam, hal ini masih jauh dari kenyataan bahwa bumi berjarak 93 juta mil dari matahari. Lubang hitam juga dapat bertambah massanya dengan cara bertubrukan dengan lubang hitam yang lain sehingga menjadi satu lubang hitam yang lebih besar.

 animasi black holes
nasa picturing the black holes
a journey of the black holes

seberapa besar kita di alam semsta